| H. E. Smith |

| Physics 11 - The Units of Science |

Introduction
It's always a good idea when you're traveling, to try and learn a few
words of the local language. So, as you set out to explore the physical
world, let me introduce you to a few words, units and "currency" that
you'll encounter on the trip.
 Scientific Notation
Scientific Notation
The important numbers in Physics span almost 40 orders of magnitude in size.
Consider the mass of the Sun:
|
It's cumbersome, to say the least, having to write out all of those zeros.
Even changing the units to metric tons (eliminate 3 zeros) doesn't
help much. Furthermore, we really don't know the Sun's mass beyond the
accuracy of the fourth digit. All those zeros are just place-keepers,
carrying no useful information.
For this reason, scientists use a short-hand called
scientific notation
to express very large or very small numbers.
In scientific notation the Sun's mass becomes:
|
 |
The number above the ten, called the power of ten or exponent,
stands for the number of decimal places. If it is positive, as in the mass of
the Sun, the decimal places are in front of the decimal point. So,
1030 means
"move the decimal point 30 places to the right and fill the empty
places with zeros" (or, more mathematically, multiply by ten 30 times).
For very small numbers, such as the mass of the proton, we use negative powers
of 10.
For negative exponents, the powers of 10 are after the decimal point; 10-27 means "move the decimal point 27 places to the left and fill in with zeros" (or divide by ten 27 times).
There are several good web pages about Scientific Notation. If you would like to read a bit more, try out the University of Maryland's Astronomy Programs site, with a Scientific Notation Exercise and an Astronomical Distance Calculator.
 Arithmetic in Scientific Notation
Arithmetic in Scientific NotationArithmetic with scientific notation is just two easy steps, as shown in the tables below.
| Multiplication |
|---|
| Step 1: Multiply numbers |
| Step 2: Add exponents |
So:
| Addition / Subtraction |
|---|
| Step 1: Convert to a common exponent |
| Step 2: Add or subtract. |
 5 x 1011
5 x 1011

The Milky Way Galaxy - count the stars if you have a bit of free time.
The mass of the sun, a typical star is about 2 x 1030
kilograms. (Your mass is about 70 kgs!)
 2 x 1030kilograms
2 x 1030kilograms
Then, the mass of the Milky Way is the number of stars times the mass of a
typical star:
 N*
x M*
N*
x M*  (5 x 1011stars) x (2 x 1030kgs)
(5 x 1011stars) x (2 x 1030kgs)
So that:
 ( 5 x 2 )
x 10 (11 + 30) kilograms
( 5 x 2 )
x 10 (11 + 30) kilograms  10 x 1041 kg = 1 x 1042 kg.
10 x 1041 kg = 1 x 1042 kg.
This is, of course, a crude estimate, especially because we now know that the mass of the Milky Way is dominated by unseen matter.
Division in Scientific Notation is just the inverse process:
| Division |
|---|
| Step 1: Divide numbers |
| Step 2: Subtract exponents |
Another example will show how it's done. Suppose you wanted to estimate the number hydrogen atoms in the sun. One estimate would be to divide the sun's mass by the mass of a hydrogen atom. (This assumes that the Sun is composed entirely of hydrogen atoms. It is mostly hydrogen, with some helium and other heavier elements thrown in.)
 Msun / mH
Msun / mH  2 x 1030kg / 1.67 x 10-27kg
2 x 1030kg / 1.67 x 10-27kg
 2 x
10-27kg) and subtract the exponent of the divisor (-27) from
the exponent of the dividend (30).
2 x
10-27kg) and subtract the exponent of the divisor (-27) from
the exponent of the dividend (30).
 (2 / 2) x 10(30-[-27])
(2 / 2) x 10(30-[-27])  1057
1057
 Units of Measurement
Units of Measurement
| Metric Prefixes | |||||
|---|---|---|---|---|---|
| PREFIX | DEFINITION | SCIENTIFIC NOTATION |
PREFIX | DEFINITION | SCIENTIFIC NOTATION |
| tera | 1,000,000,000,000 | 1012 | centi | .01 | 10-2 |
| giga | 1,000,000,000 | 109 | milli | .001 | 10-3 |
| mega | 1,000,000 | 106 | micro | .000001 | 10-6 |
| kilo | 1,000 | 103 | nano | .000000001 | 10-9 |
| deka | 10 | 101 | pico | .000000000001 | 10-12 |
| deci | .1 | 10-1 | femto | .000000000000001 | 10-15 |
Here is a list of prefixes from the National Institute of Standards and Techonology (NIST).
A few examples of how to use the metric prefixes:
Even the "world standard" metric system has different versions.
Astronomers use a version
of the cgs (Centimeter-Gram-Second)
system,
modified for the immense distances in the Universe and huge masses of
astronomical objects. Most physicists are converging on use of the MKS
(Meter-Kilogram-Second) version or Systeme Internationale (SI).
 Length
Length
To describe distances and sizes, we define a standard of length.
The SI unit of length is the meter, abbreviated
"m". A meter is a little longer than a yard (39.37 inches)
There are three special units of distance used by astronomers. These
are the astronomical unit (AU), the
light-year and the
parsec. The astronomical unit is the average distance of the Earth
from the Sun shown above.
A light-year (ly) sounds like a measure
of time, but it is a length - the distance light travels in one year.(We
can use a light-year as a unit of measure because ALL light travels at the
same speed; it is a fundamental constant of the Universe. More about this
later...) So, in one year, light travels:

The name parsec comes from the technique of measuring distance called
parallax. The nearest star, Alpha Centauri, is about 1.3 pc or
4 light-years away.
In addition to these distance units, astronomers use the
Ångstrom(Å) as a measure of size on the atomic scale.
 Mass
Mass
Everyone knows that the astronauts weigh less when they're walking on the Moon than when they're back on Earth. Since the Moon is less massive than the Earth, it's gravitational attraction is smaller. It is essential to have a unit for measuring "amount of stuff" that would be the same everywhere in the Universe. That unit of "stuff" is called mass. So, an astronaut's weight is less on the Moon, but his/her mass is exactly the same. Actually,weight and mass are two different things. Your weight is the gravitational attraction between you and the Earth. (Or whatever planet you may be visiting.) Your mass is a measure of your inertia, your resistance to changes in motion. Here is a nice explanation of mass.
The SI unit of mass is the kilogram. It is
about 10% over two pounds:
On the very large (astronomical) scale and the very small (atomic) scale two other units of mass are used. To measure atomic masses the atomic mass unit (amu) is employed. the amu is defined as one-twelfth the mass of a common carbon atom:
slightly less than the mass of a proton. For stars, galaxies, etc. we use the solar-mass

 2 x 1030kg
2 x 1030kg
where the "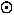 " is the standard astronomical
symbol for the sun. The mass of our Milky Way Galaxy is about
1012M
" is the standard astronomical
symbol for the sun. The mass of our Milky Way Galaxy is about
1012M .
.
 Time
Time
The MKS unit of time is the second. The
time standard is kept by the NIST using a cesium atomic clock like the
one to the right.
|
 Energy
Energy
Much of physics and astrophysics is concerned with understanding the energy generation and energy output from objects. Energy conservation principles are among the most important and useful physical tools. The SI unit of energy is the joule. A joule is the amount of energy contained in the motion of a 1 kilogram mass moving with a velocity of 1 meter/second or about the energy represented by a brick moving at 2 mph. The energy output, production, or consumption of an object is its Power, measured in joules/second or Watts. A 100-watt light bulb consumes 100W of electrical energy. A possibly more familiar unit of power, the horsepower is related by:
At the atomic / nuclear level, energies are often given in
electron-volts (abbreviated as "eV"), the
energy of an electron
accelerated through a voltage of 1 volt (1 eV =
1.6 x 10-19 joules).
The energy-levels and ionization energies of most atoms are a few eV.
X-ray photon energies are frequently quoted in
kilo-electron-volts(KeV). Gamma-rays and nuclear energies are
most often in MeV.
As stated in Einstein's formula,
 Force
Force
In nature, forces are the "pushes" that cause
masses to move.
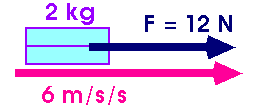 | F = ma | 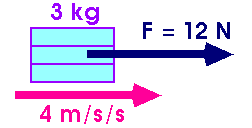 |

![]() The Scale of the Universe
The Scale of the Universe
![]() Physics 11 Lectures
Physics 11 Lectures
![]() Physics 11 Home
Physics 11 Home