General Relativity & Black Holes

| Gene Smith's Astronomy Tutorial General Relativity & Black Holes |
 |

Einstein's General Theory of Relativity
The General Theory of Relativity is an expansion of the Special Theory to include gravity as a property of space. Start with this Gravity Tutorial.
The Theory of Special Relativity has as its basic premise that light moves at a uniform speed, c = 300,000 km/s, in all frames of reference. This results in setting the speed of light as the absolute speed limit in the Universe and also produced the famous relationship between mass and energy, E = mc2. The foundation of Einstein's General Theory is the Equivalence Principle which states the equivalence between inertial mass and gravitational mass.
Inertial Mass is the quantity that determines how difficult it is to alter the motion of an object. It is the mass in Newton's Second Law:
Gravitational mass is the mass which determines how strongly two objects attract each other by gravity, e.g. the attraction of the earth:
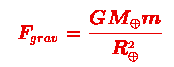
It is the apparent equivalence of these two types of mass which results in the uniformity of gravitational acceleration -- Galileo's result that all objects fall at the same rate independent of mass:
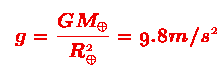
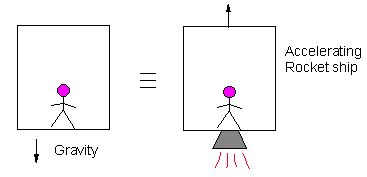
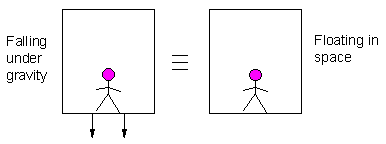
Galileo and Newton accepted this as a happy coincidence, but Einstein turned it into a fundamental principle. Another way of stating the equivalence principle is that gravitational acceleration is indistinguishable from other forms of acceleration. According to this view a student in a closed room could not tell the difference between experiencing the gravitational pull of the earth at the earth's surface and being in a rocketship in space accelerating with a = 9.8 m/s2.
nor could students in a similar room distinguish between free-fall under gravity and the weightlessness of space.
| The second fundamental principle of General Relativity is that the presence of matter curves space. In this view, gravity is not a force, as described by Newton, but a curvature in the fabric of space, and objects respond to gravity by following the curvature of space in the vicinity of a massive object. The description of the curvature of space is the mathematically complicated part of general relativity involving "metrics", which describe the way that matter curves space, and tensor calculus. |  The Curvature of Space caused by a Massive Object. |
The figure above represents a two-dimensional slice through three-dimensional space showing the curvature of space produced by a spherical object, perhaps the sun. Einstein's view is that the planets follow the curvature of space around the sun (and produce a tiny amount of curvature themselves).
Here are two fine astronomy course pages on General Relativity from Dr. Terry Herter at Cornell, from whom I stole the above images, and astronomers at the University of Tennessee.
Predictions of General Relativity
Einstein predicted several
experimental effects in which General Relativity differs from Newtonian
Gravity: 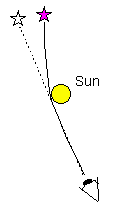
The first opportunity to test Einstein's calculation came with the Solar Eclipse of 1919. British Astrophysicist Sir Arthur Eddington mounted a pair of expeditions to West Africa and Brazil to observe the shift in position of the Hyades cluster stars behind the occulted sun. Eddington's measurements, though not perfectly precise clearly showed a deflection and favored the larger value. The result made Einstein world-famous. The test can now be made with greater precision. Every year the radio source 3C279 is occulted by the sun. Because the sun is only a modest radio-emitter, Radio Astronomers do not need to wait for an eclipse. Radio interferometry of 3C279 as it passes behind the sun has confirmed Einstein's calculation to better than 1%.
 An exciting and only very recently verified prediction of the bending of light
by gravity is the existence of
gravitational lenses; an optical lens focuses light be refraction,
bending of light due to the change of the speed of light as it passes through
a refractive medium. Because gravity can bend light, massive objects can act
as lenses, focusing and amplifying images of distant objects. Gravitational
lenses have rather different properties than "normal" lenses producing
multiple images such as the
Einstein Cross,
a case of a distant quasar imaged by a galaxy between us and the quasar,
discovered by J. Huchra & colleagues, shown to the left. If the alignment
between us, the lensing galaxy, and the distant object, an
Einstein Ring is
produced. Distant
galaxy clusters may also act as gravitational lenses. Astronomers are
beginning to make use of the gravitational lensing phenomenon to study very
distant galaxies and quasars. More about this in Lecture #17.
An exciting and only very recently verified prediction of the bending of light
by gravity is the existence of
gravitational lenses; an optical lens focuses light be refraction,
bending of light due to the change of the speed of light as it passes through
a refractive medium. Because gravity can bend light, massive objects can act
as lenses, focusing and amplifying images of distant objects. Gravitational
lenses have rather different properties than "normal" lenses producing
multiple images such as the
Einstein Cross,
a case of a distant quasar imaged by a galaxy between us and the quasar,
discovered by J. Huchra & colleagues, shown to the left. If the alignment
between us, the lensing galaxy, and the distant object, an
Einstein Ring is
produced. Distant
galaxy clusters may also act as gravitational lenses. Astronomers are
beginning to make use of the gravitational lensing phenomenon to study very
distant galaxies and quasars. More about this in Lecture #17.
Twins Bill and Jill, born within minutes of each other, take differing career paths. Jill becomes an astronaut and Bill becomes a ground-based astronomer. On their 21st birthday Jill sets out on a space mission to Aldebaran, 32 light years away. Travelling at 99.5% of the speed of light, Jill measures a time of 3.2 years for her trip to Aldebaran and another 3.2 years for her return. (Incideltally, while she is travelling near the speed of light she also sees the distance to Aldebaran contracted to a mere 3.2 light years.) Bill finds that it takes her 32 years and 2 months for each leg. Upon Jill's return, she is 27 while her sibling is 85! Bizarre as these effects appear to us slow moving mortals, relativistic time dilation has been repeatedly confirmed in high energy particle accelerators, where particles travel near the speed of light, and by atomic clock on supersonic aircraft.
A similar process occurs in the presence of strong gravity; a timekeeper in a strong gravitational field will measure a slower time than one in the absence of gravity. It is not just clocks, by the way, all physical processes: clocks ticking (however they measure their ticks), hearts beating, aging, etc., must slow down, but the only one who notices is the distant timekeeper. Everything seems "normal" to the person measuring the duration of events in his own frame of reference. Light waves travelling past the sun are slowed down by this time dilation by a small but measurable amount. In 197X the Viking Mars Lander performed the initial confirming experiment of gravitational time dilation by relaying radio signals back to earth from the Martian surface on the other side of the solar system. Although the effects of the intervening solar wind complicate the experiment, NASA scientists demonstrated clearly that the radio signals took longer on their round trip by just the amount predicted by the predicted slowing of time.
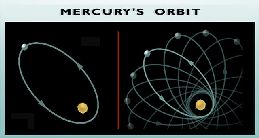 Precession of Mercury's Orbit: Kepler's first law states
that planets travel around the sun in elliptical orbits and Newton verified
this as a consequence of his law of gravity. Even in Newtonian physics this
law is not obeyed precisely, because the gravitational pull of the other
planets perturbs the orbit in a small but detectable way; It was by these
small perturbations that the planets Neptune and Pluto were discovered. It
was known well before Einstein that these effects cause the axis of the orbit
of Nercury to rotate slowly, so that its point of closest approach to the sun,
the perihelion, moves or precesses from orbit to orbit, as shown
in the figure to the right from NCSA's Relativity site. The motion is very
small - it takes a quarter of a million years for Mercury's perihelion to
complete a full circle around the sun. However, the effects of the known
planets cannot account for all of Mercury's precession. The only plausible
explanation in Newton's gravity is another planet, even closer to the sun
than Mercury. This planet, prematurely named Vulcan, was never found despite
exhaustive searches and the extra precession - about 1/100th of a degree per
century - remained a mystery. Einstein applied his General Theory to the
motion of Mercury and found that the somewhat higher gravitational pull
as the planet approaches the sun in General Relativity causes Mercury to
move a bit further around the sun each time it passes. His calculation
found exactly the observed extra precession. Because the precession of
Mercury's orbit is a direct result of the full General Theory, not just the
Equivalence Principle, Einstein viewed it as the most critical test of his
theory.
Precession of Mercury's Orbit: Kepler's first law states
that planets travel around the sun in elliptical orbits and Newton verified
this as a consequence of his law of gravity. Even in Newtonian physics this
law is not obeyed precisely, because the gravitational pull of the other
planets perturbs the orbit in a small but detectable way; It was by these
small perturbations that the planets Neptune and Pluto were discovered. It
was known well before Einstein that these effects cause the axis of the orbit
of Nercury to rotate slowly, so that its point of closest approach to the sun,
the perihelion, moves or precesses from orbit to orbit, as shown
in the figure to the right from NCSA's Relativity site. The motion is very
small - it takes a quarter of a million years for Mercury's perihelion to
complete a full circle around the sun. However, the effects of the known
planets cannot account for all of Mercury's precession. The only plausible
explanation in Newton's gravity is another planet, even closer to the sun
than Mercury. This planet, prematurely named Vulcan, was never found despite
exhaustive searches and the extra precession - about 1/100th of a degree per
century - remained a mystery. Einstein applied his General Theory to the
motion of Mercury and found that the somewhat higher gravitational pull
as the planet approaches the sun in General Relativity causes Mercury to
move a bit further around the sun each time it passes. His calculation
found exactly the observed extra precession. Because the precession of
Mercury's orbit is a direct result of the full General Theory, not just the
Equivalence Principle, Einstein viewed it as the most critical test of his
theory.
Predicted sources of strong gravitational waves in the Galaxy are supernova explosions, collapsing stellar cores as they form neutron stars or black holes, compact binary star systems, collisions of neutron stars & black holes, or possibly material falling into the blavk hole which may reside in the Galactic Center. Gravitational waves have not yet been detected directly, but we believe that they have been detected indirectly by radio astronomers in the binary pulsar system 1913+16. As the pulsar is accelerated around its companion, orbiting every 8 hours in this compact system, General Relativity predicts that gravitational waves should be produced. Although these waves are far too faint to be detected directly, the binary pulsar system is losing energy through this radiation, and the pulsar/neutron star and its companion are predicted to be slowly spiralling together. The rapid radio pulses permit precise timing of the pulsar orbit by doppler shifts of the pulse period as the pulsar moves toward or away from us. Since the discovery of the binary pulsar in 1974, timing of the pulsar has shown that the stars are indeed spiralling together just as predicted. In 300 million years the stars will coalesce - that should produce gravitational radiation that can be easily detected!
Laser interferometer observatories are being constructed that will be able to detect gravitational waves from possible sources potentially as far away as 100 million light years. A collaboration between Caltech and MIT is building LIGO, the Laser Interferometric Gravitational-Wave Observatory, to begin observations in 2000 and there are at least five other projects among European, Australian, Japanese, and Space Physicist groups constructing other Gravitational-Wave Observatories. Watch this space for News!
All of this amounts to pretty spectacular confirmation of General Relativity Theory.
So, Einstein was right and Newton was wrong!
Well, that's not really the way science works and besides, Newton was not completely wrong and Einstein is not completely right. Newton's Theory is perfectly fine for most calculations of gravity where the field is not too strong. NASA scientists do not use General Relativity to calculate the paths of spacecraft that are sent to explore the solar system (not because it would be too complicated or difficult, but because it would be a waste of time - Newton was right as far as most things in the Solar System are concerned). Furthermore, General Relativity fails on very small scales when quantum mechanical effects become important. Theoretical Physicists are working very hard on theories of "Quantum Gravity", but so far no one has succeeded in improving Einstein's Theory; no doubt the next better theory of gravity will still be an approximation of the "Truth". Science works by:
Relativity Links
Black Holes
The French mathematician LaPlace first speculated about the existence of an
object so compact that the
escape speed would be greater than the speed of
light. The first relativistic calculation was performed by
Karl Schwarzschild (1916) shortly after Einstein published his theory.
Curiously, Schwarzschild's result is the same as that of LaPlace; an object
with mass M which has a size
|
will have an escape speed equal to the speed of light. We call such an object a Black Hole. (Note that for the sun to be a black hole it would have to be compressed by a quarter of a million times down to a radius less than 3km.) A black hole is an object so compact that nothing can escape its gravity, not even light. Mathematically, a black hole is an object of zero size and infinite density (but finite mass) - a singularity. Schwarzschild's calculation shows that the gravitational radius, also called the Schwarzschild radius or event horizon, provides an effective size for a black hole because nothing can escape from inside the gravitational radius and there can be no communication from objects inside Rgrav and the outside world. | 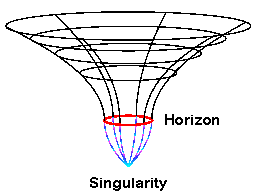 Curved Spacetime around a Black Hole. Inside the horizon or gravitational radius space is so strongly curved that nothing can escape. |
First, perhaps we should dispel a prime misapprehension about black holes:
Black holes are not gigantic vacuum cleaners sucking everything in the
Universe into their darkness. And you would have to be pretty foolish to
get caught in the strong gravity of a black hole; hopefully our interstellar
astronauts will get better training than the hapless space explorers in so
many bad sci-fi stories. This is because black holes have finite
mass and because everything in the Universe is so far apart. Black holes are
produced by massive stars as a natural part of the stellar evolutionary
process. A black hole from a collapsed 10M
 stellar core will have a mass
of 10 solar masses. It will produce gravitational effects on neighboring
stars just like a normal 10M
stellar core will have a mass
of 10 solar masses. It will produce gravitational effects on neighboring
stars just like a normal 10M star would. You need to get close
to black hole (i.e. near the gravitational radius) for its strong
gravity to "suck you in" or for General Relativistic effects to be important.
star would. You need to get close
to black hole (i.e. near the gravitational radius) for its strong
gravity to "suck you in" or for General Relativistic effects to be important.
Similarly, if you were on a planet orbiting a star which became a black hole, you would not be sucked in by the Black Hole's gravity. If the star loses no mass, you would feel no change in the gravity and would continue to stay in the same orbit. (Lots of other bad things would happen, particularly if the star goes through a supernova explosion. In that case, cosmic rays & gamma rays would extinguish life on the planet and the mass lost in the explosion would decrease the gravitational pull of the remnant causing your planet to fly off into space.)
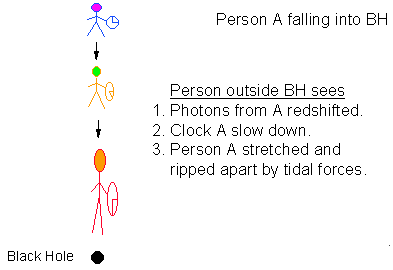 |
Should you be unfortunate enough (and foolish enough) to be sucked into a
black hole your demise would be nearly instantaneous in your reference
frame. You would first be pulled apart by intense tidal forces because
the force on your feet would be much stronger than that on your head. Then
you would be crushed into infinite density as you become part of the
singularity at the center of the black hole.
Things would appear very different to a distant observer due to the General Relativistic effects described above. Time, as measured far away, would appear to get slower and slower as you approach the gravitational radius - the distant observer would be denied the thrill of actually seeing you disappear into the black hole because time "stops" at the gravitational radius. Any signals that you send would be redshifted by increasing amounts as you near the black hole. |
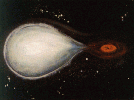
| We believe that we have found black holes in our galaxy in the form of X-Ray Binary Stars. In these star systems material may be transferred from a main sequence or red giant companion onto the black hole. (Remember that massive stars live fast & die young.) When a binary star system is formed, the more massive star will complete its life cycle first, becoming a black hole (or perhaps a neutron star). When the lower mass companion begins to expand, evolving toward the red giant phase, material may be pulled toward the black hole. Because of the angular momentum from the stars mutual orbits, the material cannot fall directly down the black hole, but spirals inward forming an accretion disk. The release of gravitational energy as material spirals into the black hole heats the accretion disk to millions of degrees so that it emits x-rays. |  Artists Conception of the Black Hole Binary Star System, Cygnus X-1. Material is pulled from the Companion into an Accretion Disk (shown in red) which is heated to millions of degrees as material spirals into the Black Hole. |
Neutron stars in binary star systems may also be x-ray binaries. Material falling from a companion onto a compact neutron star may release just about as much gravitational energy as material falling into a black hole. Neutron stars will probably be pulsars in x-rays just like in the radio. Here is a JAVA x-ray pulsar animation courtesy of the Chandra X-Ray Observatory.
The best known black hole candidate is
Cygnus X-1,
an x-ray binary in Cygnus and one of the brightest x-ray sources in the sky.
In 1972 Cygnus X-1 was identified with a 9th magnitude O supergiant,
catalogued as HDE226868. HDE226868 is orbiting an unseen companion which
orbital analysis indicates has a mass of about
20M ,
far too massive to be a neutron star or white dwarf. Cygnus X-1 also has
unusual
x-ray properties
which lend support to the idea that this must be a black hole.
,
far too massive to be a neutron star or white dwarf. Cygnus X-1 also has
unusual
x-ray properties
which lend support to the idea that this must be a black hole.
Stellar black holes have masses in the range of a few times the mass of the sun, up to a few tens of solar masses, but other processes may produce very massive black holes. There is increasing evidence that there may be a million solar mass black hole in the center of our Milky Way galaxy, and black holes with masses up to a billion times the sun's mass in the cores of other galaxies. Many astronomers also believe that black holes power quasars and other active galaxies.
Black Hole Links & References

![]() The Milky Way
The Milky Way
![]() Supernovae & Neutron Stars
Supernovae & Neutron Stars
![]() Education & Outreach
Education & Outreach
![]() CASS Home
CASS Home
Conducted by Gene Smith, CASS/UCSD.
Comments?
You may send email to hsmith@ucsd.edu
Prof. H. E. (Gene) Smith
CASS 0424 UCSD
9500 Gilman Drive
La Jolla, CA 92093-0424
Last updated: 9 March 2000